Question

Your class raised money by selling hot dogs and hamburgers. Hot dogs were sold for $.50 (fifty cents), and hamburgers were sold for $1 (one dollar). The total money raised by your class was $80. Together you sold 108 hot dogs and hamburgers. How many of each were sold?

Answer 1

Number of hot dogs sold = 56

Number of hamburgers sold = 52

Explanation:

Let

Number of hot dogs sold = x

Number of hamburgers sold = y

We can make equation from given equations:

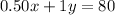`0.50x+1y=80` (Hot dogs were sold for $.50 (fifty cents), and hamburgers were sold for $1 (one dollar). The total money raised by your class was $80. )

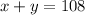`x+y=108` (Together you sold 108 hot dogs and hamburgers.)

Now we cam solve these system of equations to find value of x and y

`0.50x+y=80--eq(1)\\x+y=108--eq(2)`

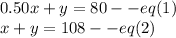
Subtract both equations to get value of x:

`0.50x+y=80\\x\:\:\:\:\:\:\:\: + y=108\\-\:\:\:\:\:\:\:\: -\:\:\:\:\:\: -\\---------\\-0.5x=-28\\x=(-28)/(-0.5)\\x=56`

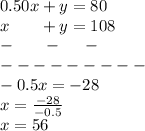
We get value of x = 56

Now putting value of x in equation 2 to find value of y

`x+y=108\\56+y=108\\y=108-56\\y=52`

So, we get y = 52

Therefore,

Number of hot dogs sold = x = 56

Number of hamburgers sold = y = 52