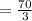Answer:
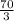
Explanation:
Given a fraction
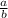 and a fraction
and a fraction
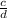 , you can find the product by multiplying the numerator of the first fraction by the numerator of the second fraction and the denominator of the first fraction by the denominator of the second one:
, you can find the product by multiplying the numerator of the first fraction by the numerator of the second fraction and the denominator of the first fraction by the denominator of the second one:
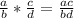
Therefore, knowing this you can find the product of the fractions
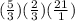 :
:
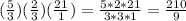
And finally you need to reduce the fraction: