Question

What is the completely factored form of x4 + 8x2 – 9?

Answer 1

`(x^2+9)(x-1)(x+1)`

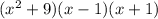
Explanation:

We would need to let u = x^2 and use middle term factorization first. let's do this:

if u = x^2, then x^4 + 8x^2 – 9 would be

u^2+8u-9

Middle term factorization of this is:

(u+9)(u-1)

now replacing back u = x^2:

(x^2+9)(x^2-1)

Using the formula a^2 - b^2 = (a+b)(a-b), we can write (x^2 - 1) as (x+1)(x-1).

So, the final factored form is: (x^2+9)(x-1)(x+1)

Answer 2

`( {x}^(2) + 9)({x} - 1)(x + 1)`

EXPLANATION

The given function is

`{x}^(4) + 8 {x}^(2) - 9`

Split the middle term

`{x}^(4) + 9 {x}^(2) - {x}^(2) - 9`

Factor by grouping;

`{x}^(2) ( {x}^(2) + 9) -1 ({x}^(2) + 9)`

Factor further to get:

`( {x}^(2) + 9)({x}^(2) - 1)`

Apply difference of two squares to get:

`( {x}^(2) + 9)({x} - 1)(x + 1)`