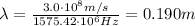Question

The Global Positioning System (GPS) network consists of 24 satellites, each of which makes two orbits around the Earth per day. Each satellite transmits a 50.0-W sinusoidal electromagnetic signal at two frequencies, one of which is 1575.42 MHz. Assume that a satellite transmits half of its power at each frequency, and that the waves travel uniformly in a downward hemisphere. a. What average intensity does a GPS receiver on the ground, directly below the satellite, receive? (Hint: for satellites in Earth orbit, the gravitational force supplies the centripetal force for the satellite to remain in orbit). b. What are the amplitudes of the electric and magnetic fields at the GPS receiver in part (a), and how long does it take the signal to reach the receiver? c. If the receiver is a square panel 1.50 cm on a side that absorbs all of the beam, what average pressure does the signal exert on it? d. What wavelength must the receiver be tuned to?

Answer 1

a)
`1.51\cdot 10^(-14) W/m^2`

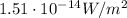
In order to calculate the average intensity, we need to calculate the distance between the satellite and Earth's surface.

The satellite makes two orbits per day, so the period is

`T=12 h = 12 h \cdot (3600 s/h)=43,200 s`

So the angular frequency is

`\omega=(2\pi)/(T)=(2\pi)/(43200 s)=1.45\cdot 10^(-4) rad/s`

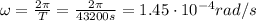
The gravitational force between the satellite and Earth provides the centripetal force that keeps the satellite in orbit:

`G(Mm)/(r^2)=m \omega^2 r`

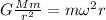
where

G is the gravitational constant

M is the Earth's mass

m is the satellite mass

R is the distance between the Earth's center and the satellite

Solving for r,

`r=\sqrt[3]{(GM)/(\omega^2)}=\sqrt[3]{((6.67\cdot 10^(-11))(5.98\cdot 10^(24) kg))/((1.45\cdot 10^(-4)rad/s)^2)}=2.67\cdot 10^7 m`

However, the distance of the satellite from Earth's surface is actually this value minus the radius of the Earth:

`h=r-R=2.67\cdot 10^7 m-6.37\cdot 10^6 m=2.30\cdot 10^7 m`

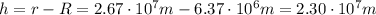
The waves travel in a downward hemisphere, so the area of the surface of propagation is

`A=2 \pi h^2 = 2\pi (2.30\cdot 10^7 m)^2=3.32\cdot 10^(15) m^2`

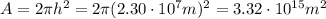
And since the power is

P = 50.0 W

We can now calculate the intensity:

`I=(P)/(A)=(50.0 W)/(3.32\cdot 10^(15) m^2)=1.51\cdot 10^(-14) W/m^2`

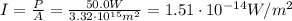
b)
`3.37\cdot 10^(-6) V/m, 1.12\cdot 10^(-14)T`, 0.077 s

The average intensity of an electromagnetic wave is given by

`I=(1)/(2)c \epsilon_0 E^2`

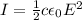
where

c is the speed of light

`\epsilon_0` is the vacuum permittivity

E is the amplitude of the electric field

Solving for E, we find

`E=\sqrt{(2I)/(c\epsilon_0)}=\sqrt{(2(1.51\cdot 10^(-14) W/m^2))/((3\cdot 10^8 m/s)(8.85\cdot 10^(-12) F/m))}=3.37\cdot 10^(-6) V/m`

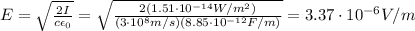
The amplitude of the magnetic field is given by

`B=(E)/(c)=(3.37\cdot 10^(-6) V/m)/(3.0\cdot 10^8 m/s)=1.12\cdot 10^(-14)T`

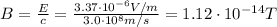
And since the waves travels at speed of light and the distance is h, the time thay take to reach the receiver is

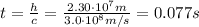
`t=(h)/(c)=(2.30\cdot 10^7 m)/(3.0\cdot 10^8 m/s)=0.077 s`

c)
`5.03\cdot 10^(-23)Pa`

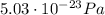
In case of a perfect absorber, the radiation pressure due to an electromagnetic wave is given by

`p=(I)/(c)`

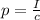
where

I is the intensity of the wave

c is the speed of light

Here we have

`I=1.51\cdot 10^(-14) W/m^2`

`c=3.0\cdot 10^8 m/s`

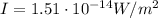
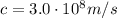
So the average pressure is

`p=(1.51\cdot 10^(-14) W/m^2)/(3.0\cdot 10^8 m/s)=5.03\cdot 10^(-23)Pa`

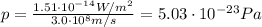
d) 0.190 m

The receiver must be tune on the same wavelength of the emitter.

The wavelength of an electromagnetic wave is

`\lambda=(c)/(f)`

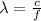
where

c is the speed of light

f is the frequency

The frequency of the waves emittted by the satellite is

`f=1575.42 MHz=1575.42\cdot 10^6 Hz`

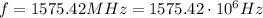
so the wavelength is

`\lambda=(3.0\cdot 10^8 m/s)/(1575.42\cdot 10^6 Hz)=0.190 m`