Answer:
Option 1.
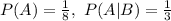 Dependent
Dependent
Option 2
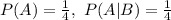 Independent
Independent
Option 3
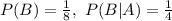 Dependent
Dependent
Option 4
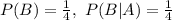 Independent
Independent
Explanation:
Two events A and B are independent if the occurrence of A does not affect the probability of B.
On the other hand The probability of A given B is defined as:
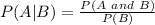
When two events are independent then:
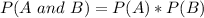
So if the two events A and B are independent this means that:
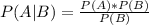

Which makes sense because if the events are independent then the probability of A not being affected by B.
So to solve this problem identify in what cases
 or
or
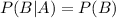
When this happens those events are independent
Option 1.
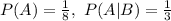 Dependent
Dependent
Option 2
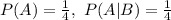 Independent
Independent
Option 3
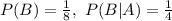 Dependent
Dependent
Option 4
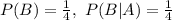 Independent
Independent