Answer: A and B are independent events if P(A∩B)=P(A).P(B)=0.15.
Explanation:
Let A be the event that a shopper buys bread.
Let B be the event that a shopper buys cheese.
So, P(A∪B)=100
Probability that a shopper buys bread during a visit to the grocery store =n 0.60
P(A) = 0.60
Similarly, Probability that a shopper buys bread = 0.25
P(B) = 0.25
Since A and B are independent then,
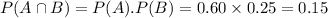
So, A and B are independent events if P(A∩B)=P(A).P(B)=0.15.