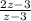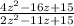Question

What is the simplified form of 4z^2-16z+15/ 2z^2-11z+15

Answer 1

`(4z^2-16z+15)/(2z^2-11z+15)` Factor the numerator and the denominator

[ax² + bx + c]

4z² - 16z + 15 Since a > 1, multiply a and c together, then find the factors of (a·c), that adds or subtracts to = b.

(a·c) --> (4 · 15) = 60

Factors of 60:

1 · 60, 2 · 30, 3 · 30, 4 · 15, 5 · 12, 6 · 10

[The only factor is 6 and 10, (-6) + (-10) = -16] So you substitute -6z - 10z for -16z

4z² - 6z - 10z + 15 Factor out 2z from 4z² - 6z, and factor out -5 from -10z + 15

2z(2z - 3) - 5(2z - 3) Factor out (2z - 3) and your left with:

(2z - 3)(2z - 5)

Do the same for the denominator, and you should get (z - 3)(2z - 5)

Now you have:

`((2z - 3)(2z-5))/((z-3)(2z - 5))` You can cancel out (2z - 5)

`(2z - 3)/(z-3)`

Answer 2

`((2z-3))/((z-3))`

Step-by-step explanation

The given expression is:

`(4z^2-16z+15)/(2z^2-11z+15)`

Let us split the middle terms to get,

`(4z^2-6z - 10z+15)/(2z^2-6z - 5z+15)`

Factor by grouping:

`(2z(2z-3) - 5(2z - 3))/(2z(z-3) - 5(z - 3))`

Factor further:

`((2z - 5)(2z-3))/((2z - 5)(z-3))`

We cancel the common factors,

`((2z-3))/((z-3))`

where

`z \\e (5)/(2) \: or \: z \\e3`