Question

Solve the system of equations below using a matrix equation.

2x + y = - 7

x − y = 4

Select one:

a.
( 1, 5 )


b.
( - 1, - 5 )


c.
( - 1, -2 )


d.
( 0, - 7 )

Answer 1

Answer: B. (-1, -5)

Explanation:

Given equations

2x + y = -7

x - y = 4

Concept

`A^(-1)=(1)/(ad-bc)\left[\begin{array}{ccc}a&b\\c&d\\\end{array}\right]`

`A*A^(-1)=A^(-1)*A=I~(Which~is~basically~1)`

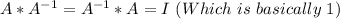
Convert into matrix

`\left[\begin{array}{ccc}2&1\\1&-1\\\end{array}\right] \left[\begin{array}{ccc}x\\y\\\end{array}\right]=\left[\begin{array}{ccc}-7\\4\\\end{array}\right]`

Calculate the inverse of the matrix

`A=\left[\begin{array}{ccc}2&1\\1&-1\\\end{array}\right]`

`A^(-1)=(1)/(ad-bc)\left[\begin{array}{ccc}a&b\\c&d\\\end{array}\right]`

`A^(-1)=-(1)/(3) \left[\begin{array}{ccc}-1&-1\\-1&2\\\end{array}\right]`

Solve by multiplying the inverse of the matrix

`A*A^(-1)=A^(-1)*A=I`

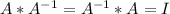
`-(1)/(3) \left[\begin{array}{ccc}-1&-1\\-1&2\\\end{array}\right]\left[\begin{array}{ccc}2&1\\1&-1\\\end{array}\right] \left[\begin{array}{ccc}x\\y\\\end{array}\right]=-(1)/(3) \left[\begin{array}{ccc}-1&-1\\-1&2\\\end{array}\right]\left[\begin{array}{ccc}-7\\4\\\end{array}\right]`

`1*\left[\begin{array}{ccc}x\\y\\\end{array}\right]=-(1)/(3)\left[\begin{array}{ccc}3\\15\\\end{array}\right]`

Simplify by multiplication

`\left[\begin{array}{ccc}x\\y\\\end{array}\right]=\left[\begin{array}{ccc}-1\\-5\\\end{array}\right]`

Therefore, the answer is
`\Large\boxed{(-1,~-5)}`

Hope this helps!! :)

Please let me know if you have any questions

Answer 2

Answer is b. (-1, -5)
Step by step
Substitute the x and y values into both equations to find equality

Answer b. Makes both equations equal

2x + y = -7

2(-1) + (-5) = -7
-2 -5 = -7
-7 = -7
It equals now let’s do the 2nd one

x - y = 4
-1 -(-5) = 4
4 = 4
This one equals too. I did the math on the other three answers and they did not equal.

Problem solved!