Answer: B. (-1, -5)
Explanation:
Given equations
2x + y = -7
x - y = 4
Concept
![A^(-1)=(1)/(ad-bc)\left[\begin{array}{ccc}a&b\\c&d\\\end{array}\right]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/ld21plysek0ksja6xpfo.png)

Convert into matrix
![\left[\begin{array}{ccc}2&1\\1&-1\\\end{array}\right] \left[\begin{array}{ccc}x\\y\\\end{array}\right]=\left[\begin{array}{ccc}-7\\4\\\end{array}\right]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/b51gklf4z08cx0mvnyst.png)
Calculate the inverse of the matrix
![A=\left[\begin{array}{ccc}2&1\\1&-1\\\end{array}\right]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/45gu98vz65w8n35fa702.png)
![A^(-1)=(1)/(ad-bc)\left[\begin{array}{ccc}a&b\\c&d\\\end{array}\right]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/ld21plysek0ksja6xpfo.png)
![A^(-1)=-(1)/(3) \left[\begin{array}{ccc}-1&-1\\-1&2\\\end{array}\right]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/hq38744w4yvajrljo6st.png)
Solve by multiplying the inverse of the matrix
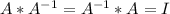
![-(1)/(3) \left[\begin{array}{ccc}-1&-1\\-1&2\\\end{array}\right]\left[\begin{array}{ccc}2&1\\1&-1\\\end{array}\right] \left[\begin{array}{ccc}x\\y\\\end{array}\right]=-(1)/(3) \left[\begin{array}{ccc}-1&-1\\-1&2\\\end{array}\right]\left[\begin{array}{ccc}-7\\4\\\end{array}\right]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/g11e86euzovkl9hjtfg6.png)
![1*\left[\begin{array}{ccc}x\\y\\\end{array}\right]=-(1)/(3)\left[\begin{array}{ccc}3\\15\\\end{array}\right]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/2hq9qg3ldn4w2s25kfdq.png)
Simplify by multiplication
![\left[\begin{array}{ccc}x\\y\\\end{array}\right]=\left[\begin{array}{ccc}-1\\-5\\\end{array}\right]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/8iw9ksz9tqzgni4l2fvh.png)
Therefore, the answer is

Hope this helps!! :)
Please let me know if you have any questions