Answer:
Second option
g(x), and the maximum is 5.’
Explanation:
In the graph it can easily be seen that the maximum value reached by the function f(x) is y = 3.
Then, the function g (x) is:
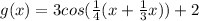
By definition the function
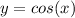 reaches its maximum value when x = 0,
reaches its maximum value when x = 0,
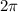 ,
,
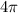 , ...,
, ...,
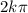
So
When
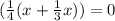 entonces
entonces
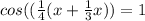 .
.
Thus:
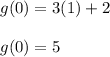 .
.
Therefore the function that has the greatest maximum is g(x) when
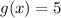
The answer is the second option