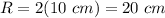Answer:
20 cm
Explanation:
Look at the picture.
The formula of a radius of a circle circumscribed around an equaliteral triangle:
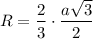
The formula od a radius of a circle inscribed into an equaliteral triangle:
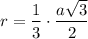
As you can see in the formulas above, the radius of the circumscribed circle is twice the radius of the inscribed circle.
Therefore
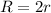
Given:
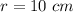
therefore