Question

A theme park charges a flat fee of $500 for group bookings of more than 25 tickets, plus $20 per ticket for up to 100 tickets and $17 per ticket thereafter. If x represents the number of tickets sold under the group booking option, complete the limit equation that represents the average cost per ticket

Answer 1

`\lim_(x \to \infty) (2500+17(x-100))/(x)=17`

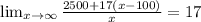
Explanation:

Let the theme park sold number of tickets = x

Theme park charges $500 for group booking more than 25 tickets.

In addition to this theme park charges $20 per ticket for up to 100 tickets.

So charges of 100 tickets = 500 + (100×20) = $2500

For more than 100 tickets theme park charges $17, so charges for x tickets will be = 500 + (100×20) + 17(x - 100)

= 2500 + 17(x - 100)

Cost of one ticket of the theme park =
`(2500+17(x-100))/(x)`

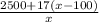
Now we have to write the limit equation when number of tickets purchased becomes very high.

`\lim_(x \to \infty) (2500+17(x-100))/(x)=17`

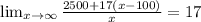
[By solving limit as below

`\lim_(x \to \infty) (2500+17(x-100))/(x)= \lim_(x \to \infty)(2500)/(x)+17-(1700)/(x)`

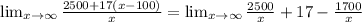
since
`\lim_(x \to \infty)((1)/(x))=0`

Therefore,
`\lim_(x \to \infty)(2500)/(x)+17-(1700)/(x)=0+17-0`

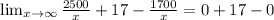
= 17 ]