Question

Write the quadratic function f(x) = x2 - 5x + 3 in vertex form.

A) f(x) = (x - 2.5)2 + 3
B) f(x) = (x + 2.5)2 + 3
C) f(x) = (x - 2.5)2 - 3.25
D) f(x) = (x + 2.5)2 - 3.25

Answer 1

C.
`f(x) = (x-2.5)^(2)-3.25`

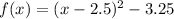
Explanation:

The vertex form for a quadratic function is:

`f(x) = a(x-h)^2+k`

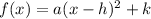
• Then, you expand the binomial and get:

`f(x) = a(x^2-2hx +h^2) + k`

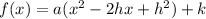
• Now you distribute and get the first form:

`f(x) = ax^2-2ahx +ah^2 + k`

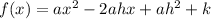
• You know that the general form for a quadratic function is:

`f(x) = ax^2+bx+c, Second\ form`

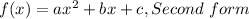
• You compare the two forms that you have and finding h and k:

`ax^2+2ahx +ah^2 + k = ax^2+bx+c`

• Finding h from the coefficient of X:

`-2ah = b`

`h = -(b)/(2a)`

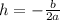
from the quadratic function given you know that a = 1 , b = -5 and c = 3, thus:

`h = -((-5))/(2(1))=2.5`

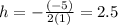
• Finding k from the third coefficient:

`ah^2+k = c`

`Isolate\ k =>\ k = c-ah^2`

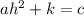
You know c,a and h, so replace the values:

`k = 3-(1)(2.5)^2 \\ k = 3-6.25\\ k = -3.25\\`

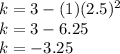
• Finally replace the values for a, h and k in the vertex form:

`f(x) = a(x-h)^2+k\\ f(x) = (1)(x-2.5)^2+(-3.25)\\ f(x) = (x-2.5)^2-3.25`

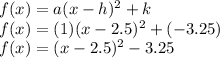
So answer is C.
`f(x) = (x-2.5)^2-3.25`