Question

If
`f(x)=(3)/(x+2) -√(x-3)`, complete the following statement:

The domain for f(x) is all real numbers ___ than or equal to 3.

Answer 1

"greater"

Explanation:

The domain is the set of x values for which a function is defined.

When we have a square root is a function, we need to remember that square root can't be negative. Thus, anything under the root would need to be GREATER THAN or EQUAL to 0.

Thus

x - 3 ≥ 0

x ≥ 3

This is the constraint.

Thus

the _____ would be "greater"

Answer 2

The domain for f(x) is all real numbers greater than or equal to 3.

Explanation:

`f(x)= (3)/(x+2) - √(x-3)`

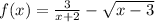
To solve the above equation, the value of x should be greater than or equal to 3, as we have the term
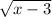`√(x-3)` and if value is less than 3, the term inside the square root will be negative and we cannot find the square root of negative numbers.

So, The domain for f(x) is all real numbers greater than or equal to 3.