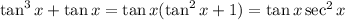12. Recall the half-angle identity,
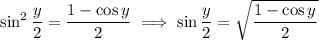
where we take the positive square root because
 is an angle in a right triangle, which means
is an angle in a right triangle, which means
 , so
, so
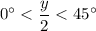 . For such an angle, it's always the case that
. For such an angle, it's always the case that
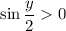 .
.
Use the Pythagorean theorem to find the length of the hypotenuse:
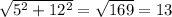
Then
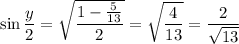
###
13.
 is in quadrant II, which means
is in quadrant II, which means
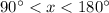 , so
, so
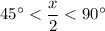 . In other words,
. In other words,
 is in quadrant I, so
is in quadrant I, so
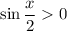 . From the half-angle identity we get
. From the half-angle identity we get
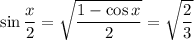
###
14. Simplification follows from the definitions of each function:
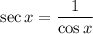
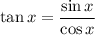
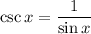
So we have
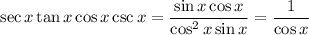
###
15. Use the Pythagorean identity:
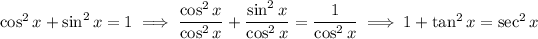
Then