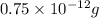Question

Carbon-14 emits beta radiation and decays with a half-life (t ) of 5730 years. Assume that you start with a mass of 6.00 × 10^–12 g of carbon 14. How many grams of the isotope remains at the end of three half-lives?

Answer 1

did you ever find the answer

Step-by-step explanation:

Answer 2

Answer:
`0.75* 10^(-12)`

Step-by-step explanation:

Formula used :

`a=(a_o)/(2^n)`

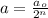
where,

a = amount of reactant left after n-half lives = ?

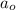`a_o` = Initial amount of the reactant =
`6* 10^(-12) g`

n = number of half lives = 3

Putting values in above equation, we get:

`a=(6* 10^(-12) )/(2^3)`

`a=(6* 10^(-12) )/(8)`

`a=0.75* 10^(-12)`

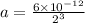
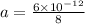
Therefore, the amount of carbon-14 left after 3 half lives will be
`0.75* 10^(-12)g`