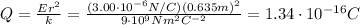Question

The 9-inch-long elephant nose fish in the Congo River generates a weak electric field around its body using an organ in its tail. When small prey, or even potential mates, swim within a few feet of the fish, they perturb the electric field. The change in the field is picked up by electric sensor cells in the skin of the elephant nose. These remarkable fish can detect changes in the electric field as small as 3.00 μN/C. How much charge, modeled as a point charge, in the fish would be needed to produce such a change in the electric field at a distance of 63.5 cm ?

Answer 1

`1.34\cdot 10^(-16) C`

Step-by-step explanation:

The strength of the electric field produced by a charge Q is given by

`E=k(Q)/(r^2)`

where

Q is the charge

r is the distance from the charge

k is the Coulomb's constant

In this problem, the electric field that can be detected by the fish is

`E=3.00 \mu N/C = 3.00\cdot 10^(-6)N/C`

and the fish can detect the electric field at a distance of

`r=63.5 cm = 0.635 m`

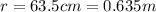
Substituting these numbers into the equation and solving for Q, we find the amount of charge needed:

`Q=(Er^2)/(k)=((3.00\cdot 10^(-6) N/C)(0.635 m)^2)/(9\cdot 10^9 Nm^2 C^(-2))=1.34\cdot 10^(-16) C`