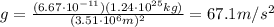Question

One model for a certain planet has a core of radius R and mass M surrounded by an outer shell of inner radius R, outer radius 2R, and mass 4M. If M = 2.48 × 1024 kg and R = 1.17 × 106 m, what is the gravitational acceleration of a particle at points (a) R and (b) 3R from the center of the planet?

Answer 1

(a) 120.8 m/s^2

The gravitational acceleration at a generic distance r from the centre of the planet is

`g=(GM')/(r^2)`

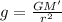
where

G is the gravitational constant

M' is the mass enclosed by the spherical surface of radius r

r is the distance from the centre

For this part of the problem,

`r=R=1.17\cdot 10^6 m`

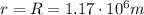
so the mass enclosed is just the mass of the core:

`M'=M=2.48\cdot 10^(24)kg`

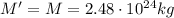
So the gravitational acceleration is

`g=((6.67\cdot 10^(-11))(2.48\cdot 10^(24)kg))/((1.17\cdot 10^6 m)^2)=120.8 m/s^2`

(b) 67.1 m/s^2

In this part of the problem,

`r=3R=3(1.17\cdot 10^6 m)=3.51\cdot 10^6 m`

and the mass enclosed here is the sum of the mass of the core and the mass of the shell, so

`M'=M+4M=5M=5(2.48\cdot 10^(24)kg)=1.24\cdot 10^(25)kg`

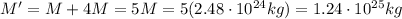
so the gravitational acceleration is

`g=((6.67\cdot 10^(-11))(1.24\cdot 10^(25)kg))/((3.51\cdot 10^6 m)^2)=67.1 m/s^2`