Answer:
Option B - Time taken for the ball to hit the ground is 2.47 seconds.
Explanation:
Given : A ball is thrown with a slingshot at a velocity of 110 ft./sec. at an angle 20 degrees above the ground from a height of 4.5 ft.
To find : How long does it take for the ball to hit the ground?
Solution :
According to question,
The equation that models the height of the ball in feet as a function of time is
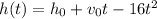
Where,
 is the initial height,
is the initial height,
 is the initial velocity and
is the initial velocity and
t is the time in seconds.
We have given,
Initial height,

A ball is thrown with a slingshot at a velocity of 110 ft./sec. at an angle 20 degrees.
The initial speed,
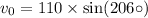

We have to find the time for the ball to hit the ground i.e. h(t)=0
Substitute all the values in the formula,
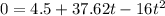
Applying quadratic formula to solve the equation,
The solution of quadratic general equation
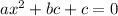 is
is
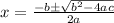
Where, a=-16 , b=37.62 , c=4.5
Substituting in the formula,
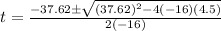
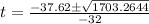
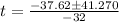
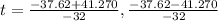

neglecting the negative value
t=2.47 seconds
Therefore,Option B is correct.
Time taken for the ball to hit the ground is 2.47 seconds.