Question

Solve the system and write your answer as a coordinate point. I

(1 Point)
-6x – 3y = 24
4x – 2y = 8

Answer 1

The solution of the system is:

(x, y) = (-1, -6)

Explanation:

Given the system of equations

-6x – 3y = 24

4x – 2y = 8

solving the system of equations

`\begin{bmatrix}-6x-3y=24\\ 4x-2y=8\end{bmatrix}`

`\mathrm{Multiply\:}-6x-3y=24\mathrm{\:by\:}2\:\mathrm{:}\:\quad \:-12x-6y=48`

`\mathrm{Multiply\:}4x-2y=8\mathrm{\:by\:}3\:\mathrm{:}\:\quad \:12x-6y=24`

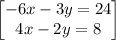
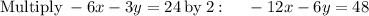
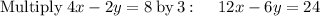
so

`\begin{bmatrix}-12x-6y=48\\ 12x-6y=24\end{bmatrix}`

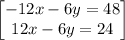
adding the equations

`12x-6y=24`

`+`

`\underline{-12x-6y=48}`

`-12y=72`

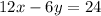
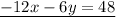
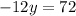
so the system of equations becomes

`\begin{bmatrix}-12x-6y=48\\ -12y=72\end{bmatrix}`

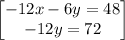
solve -5y=72 for y

`-12y=72`

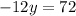
Divide both sides by -12

`(-12y)/(-12)=(72)/(-12)`

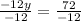
Simplify

`y=-6`

`\mathrm{For\:}-12x-6y=48\mathrm{\:plug\:in\:}y=-6`

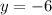
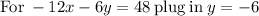
solving

`-12x-6\left(-6\right)=48`

`-12x+6\cdot \:6=48`

`-12x+36=48`

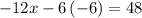
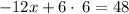
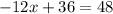
subtract 36 from both sides

`-12x+36-36=48-36`

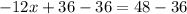
Simplify

`-12x=12`

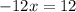
Divide both sides by -12

`(-12x)/(-12)=(12)/(-12)`

`x=-1`

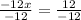
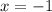
Therefore, the solution of the system is:

(x, y) = (-1, -6)