Answer:
It is clear that both equations are identical. Hence, the solution to the system of equations would contain infinitely many solutions.
Explanation:
Given the system of equations
y = -4x + 2
y = -4x + 2
It is clear that both equations are identical. We know that when the system of equations is identical, then the system of equations will have infinitely many solutions.
Hence the given system of equations would contain infinitely many solutions.
solving the system of equations
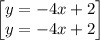
Substitute y = -4x+2
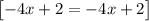
For y = -4x+2
Express y in terms of x
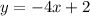
Thus, the solution to the system of equations would be:
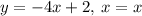
It is clear that x = x is true no matter what. Hence, the solution to the system of equations would contain infinitely many solutions.