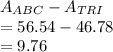Answer:
B. 9.76 u²
Explanation:
First calculate the area of the 60° wedge of the circle by calculating the area of the full circle and multiplying it by a fraction of 60°/360°:

Now calculate the the area of the white triangle in the wedge, by using a base length of
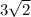 , and height:
, and height:
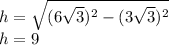
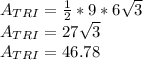
Find the area of the red segment: