Question

Describe the relationship between the terms in each arithmetic sequence. Then write the next three terms in the sequence.

0.4, 0.8, 1.2, 1.6, ...

Answer 1

Please check the explanation.

Explanation:

Given the sequence

0.4, 0.8, 1.2, 1.6, ...

An Arithmetic sequence has a constant difference 'd' and is defined by

`a_n=a_1+\left(n-1\right)d`

Computing the differences of all the adjacent terms

`0.8-0.4=0.4,\:\quad \:1.2-0.8=0.4,\:\quad \:1.6-1.2=0.4`

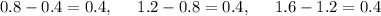
The difference between all the adjacent terms is the same and equal to

`d=0.4`

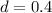
As the first element of the sequence is

`a_1=0.4`

Thus, the relationship between the terms in each arithmetic sequence can be determined by using the formula

`a_n=a_1+\left(n-1\right)d`

substituting
`a_1=0.4`, and
`d=0.4`

`a_n=0.4\left(n-1\right)+0.4`

`a_n=0.4n`

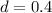
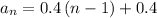
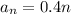
Therefore, the relationship between the terms in each arithmetic sequence is:

• 
  `a_n=0.4n`

Finding the next three terms:

Given the sequence

`a_n=0.4n`

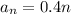
putting n = 5 to determine the 5th term

`a_5=0.4\left(5\right)`

`a_5=2`

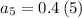
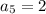
putting n = 6 to determine the 6th term

`a_6=0.4\left(6\right)`

`a_6=2.4`

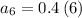
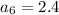
putting n = 7 to determine the 7th term

`a_7=0.4\left(7\right)`

`a_7=2.8`

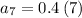
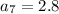
Therefore, the next three terms are:

• 
  `a_5=2`

• 
  `a_6=2.4`

• 
  `a_7=2.8`