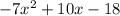Answer:
Final answer in simplified form is
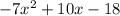
Explanation:
Given expression is
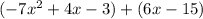
Now we need to find an equivalent expression for
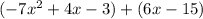
First we can distribute the positive sign and remove the parenthesis the combine like terms
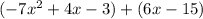
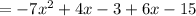
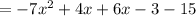
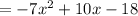
Hence final answer in simplified form is