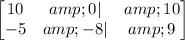Question

Write the augmented matrix for each system of equations. 10x=10 -5x-8y=9​

Answer 1

The augmented matrix is:

`\begin{bmatrix}10 & 0| & 10\\ -5 &-8| & 9\end{bmatrix}`

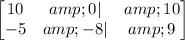
Explanation:

The steps of an augmented matrix are as follows:

• We write a matrix such that the first column of the matrix is coefficient of x in the matrix.

• The second column of the matrix is the coefficient of y in each equations.

• and then it is separated by a line and then the third column written with the help of a constant term on the right side of the equation when it is written down.

The system of equation is:

`10x=10\\and\\-5x-8y=9`

Hence, the system could be written in the form:

`AX=b`

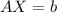
where:

`A=\left[\begin{array}{ccc}10&0\\-5&-8\end{array}\right]`

`X=\left[\begin{array}{ccc}x\\y\end{array}\right]`

and

`b=\left[\begin{array}{ccc}10\\9\end{array}\right]`

Hence, the augmented matrix is:

`\begin{bmatrix}10 & 0| & 10\\ -5 &-8| & 9\end{bmatrix}`

Answer 2

`\left[ { \begin {array} {cc} 10&0& | 10\\-5&-8& | 9\\ \end {array}} \right]`

EXPLANATION

The given system of equations is

10x=10

-5x-8y=9

We can rewrite this as:

10x+0y=10

-5x-8y=9

The augmented matrix is the combination of the coefficient matrix and the constant matrix.

The coefficient matrix is

`\left[ { \begin {array} {cc} 10&0\\ - 5& - 8\\ \end {array}} \right]`

The constant matrix is

`\binom{10}{9}`

The augmented matrix is

`\left[ { \begin {array} {cc} 10&0& | 10\\-5&-8& | 9\\ \end {array}} \right]`