Question

Integral of below.

ſ√y . e^-y^3​

Answer 1

Assuming you're equipped with the error function,

`\mathrm{erf}(x)=\displaystyle\frac2{\sqrt\pi}\int_0^x e^(-u^2)\,\mathrm du`

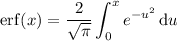
whose derivative is

`(\mathrm d)/(\mathrm dx)\mathrm{erf}(x)=\frac2{\sqrt\pi}e^(-x^2)`

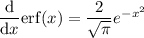
by substituting x = √y, so that x ² = y and 2x dx = dy, we have

`\displastyle\int\sqrt y e^(-y^3)\,\mathrm dy=\int 2x^2 e^(-x^6)\,\mathrm dx`

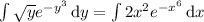
Then if u = x ³ and du = 3x ² dx, we have

`\displaystyle\int\sqrt y e^(-y^3)\,\mathrm dy=\int\frac23 e^(-u^2)\,\mathrm du`

`\displaystyle\int\sqrt y e^(-y^3)\,\mathrm dy=\frac{\sqrt\pi}3\mathrm{erf}(u)+C`

`\displaystyle\int\sqrt y e^(-y^3)\,\mathrm dy=\frac{\sqrt\pi}3\mathrm{erf}(x^3)+C`

`\displaystyle\int\sqrt y e^(-y^3)\,\mathrm dy=\boxed{\frac{\sqrt\pi}3\mathrm{erf}\left(y^(\frac32)\right)+C}`

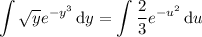
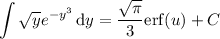
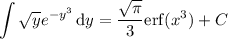
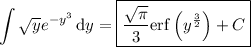
If you're not familiar with the error function, unfortunately there is no elementary antiderivative...