Question

36) The ratio of Slade's stickers to Corbett's stickers is 5: 2. If Corbett

has 27 fewer stickers than Slade, how many stickers do they have
in all?

Answer 1

63 stickers

Explanation:

Define the variables:

• Let x be the number of stickers Slade had.

• If Corbett has 27 fewer stickers than Slade:
  ⇒ Corbett = x - 27

Given ratio:

Slade : Corbett = 5 : 2

Substitute the defined variables:

`\implies \sf x : x - 27 = 5 : 2`

`\implies \sf (x)/(x-27)=(5)/(2)`

Cross multiply:

`\implies \sf 2x=5(x-27)`

Expand:

`\implies \sf 2x=5x-135`

Subtract 5x from both sides:

`\implies \sf -3x=-135`

Multiply both sides by -1:

`\implies \sf 3x=135`

Divide both sides by 3:

`\implies \sf x=45`

Therefore, Slade had 45 stickers.

Substitute the found value of x into the expression for the number of stickers Corbett had:

`\implies \sf 45-27=18`

Therefore, Corbett had 18 stickers.

Total number of stickers = 45 + 18 = 63

Answer 2

Answer: 63 Stickers

Explanation:

Given information:

Ratio = Slade : Corbett = 5 : 2

Corbett has 27 fewer stickers

Set variables:

Let x be the number of stickers Corbett has

Let x + 27 be the number of stickers Slade has

Set proportional equation:

`(2)/(5)~ =~(x)/(x~+~27)`

Cross multiply the system

`2~(x~+~27)~=~5~*~x`

Simplify by distributive property

`2~*~x~+~2~*~27~=~5x`

`2x~+~54~=~5x`

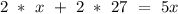
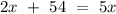
Subtract 2x on both sides

`2x~+~54~-~2x~=~5x~-~2x`

`54~=~3x`

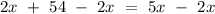
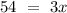
Divide 3 on both sides

`54~/~3~=~3x~/~3`

`{x=18}`

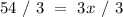
Add Corbett's and Slade's amounts together

Corbett = x = 18 stickers

Slade = x + 27 = 18 + 27 = 45 stickers

Total = 18 + 45 =
`\Large\boxed{63~Stickers}`

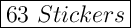
Hope this helps!! :)

Please let me know if you have any questions