Answer: 63 Stickers
Explanation:
Given information:
Ratio = Slade : Corbett = 5 : 2
Corbett has 27 fewer stickers
Set variables:
Let x be the number of stickers Corbett has
Let x + 27 be the number of stickers Slade has
Set proportional equation:
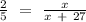
Cross multiply the system
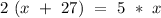
Simplify by distributive property
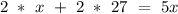
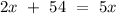
Subtract 2x on both sides
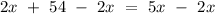
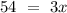
Divide 3 on both sides
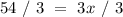
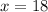
Add Corbett's and Slade's amounts together
Corbett = x = 18 stickers
Slade = x + 27 = 18 + 27 = 45 stickers
Total = 18 + 45 =
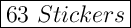
Hope this helps!! :)
Please let me know if you have any questions