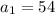ANSWER
See explanation
EXPLANATION
Question 1:
The third term of the arithmetic sequence is :
14=a+2d...(1)
The twelveth term is
59=a+11d...(2)
Subtract equation (1) from (2)
45=9d
This implies that
d=5
a=14-2(5)=4
The explicit rule is;
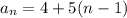
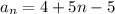
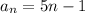
Recursive formula:
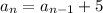
Question 2
The geometric sequence has the fourth term to be 2 and the common ratio to be r=⅓
This implies that,
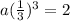
This implies that,
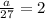
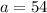
The explicit rule:
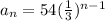
The recursive rule is
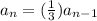
where,