Answer:
The width of the sidewalk is 5.0 ft.
Explanation:
Given,
The dimension of the rectangular swimming pool is 16 ft × 10 ft,
So, the area of the pool = 16 × 10 = 160 ft²,
Let x be the uniform width of the cement sidewalk,
So, the dimension of the area covered by both swimming pool and sidewalk = (16+x) ft × (10+x) ft,
Thus, the combined area of the swimming pool and sidewalk = (16+x)(10+x) ft²
Also, the area of the sidewalk = The combined area - Area of the pool,
= (16+x)(10+x) - 160
According to the question,
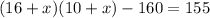

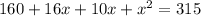
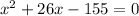
By the quadratic formula,


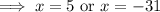
Side can not be negative,
Hence, the width of the sidewalk is 5.0 ft.