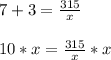Question

I am confused. Can somebody explain this to me?

Maryann can paint a wall in 45 minutes. It takes her brother Junior 1 hour and 45 minutes to paint the same wall. How many minutes would it take Maryann and Junior to paint the wall, if they work together? Answer as a decimal to the nearest tenth.

Answer 1

Answer: If they worked together, it would take 31.5 minutes

Explanation:

There's a certain formula for equations like this:

`(1)/(t1) +(1)/(t2)=(1)/(tb)`

t1= the time it took for the first person to complete the task.

t2= the time it took for the second person to complete the task.

tb= the time it took for both of them to complete the task.

We have the values for both t1 and t2, but not for tb.

t1= 45

t2= 105

tb= x

`(1)/(45) +(1)/(105) = (1)/(x)`

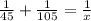
Now it's simple algebra, and all we need to do is solve for x

The LCM for both fractions is 315, so now we multiply BOTH sides of the equation by 315.

`(315)/(45) + (315)/(105) = (315)/(x)`

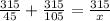
This will simplify nicely, so now we just need to get x on the other side.
`7 + 3 = (315)/(x) \\\\\ 10*x = (315)/(x) * x`

`10x = 315 \\\\x = 31.5`