Question

Which geometric series converges ???

Answer 1

Answer: The correct option is

(C)
`\sum_(n=1)^(\infty)4(-0.2)^(n-1).`

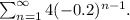
Step-by-step explanation: We are give to select the geometric series that converges.

We know that

the general (n-th) term of a common geometric series is given by

`a_n=ar^(n-1).`

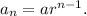
And the series converges if the modulus of the common ratio is less than 1, .e., |r| < 1.

Now, for the first infinite geometric series, we have

`a_n=(2)/(3)(-3)^(n-1).`

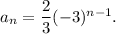
So, the common ratio will be

`r=-3~~~\Rightarrow |r|=3>1.`

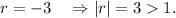
That is, the series will not converge. Option (A) is incorrect.

For the second geometric series, we have

`a_n=5(-1)^(n-1).`

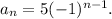
So, the common ratio will be

`r=-1~~~\Rightarrow |r|=1.`

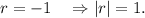
That is, the series will not converge. Option (B) is incorrect.

For the third geometric series, we have

`a_n=4(-0.2)^(n-1).`

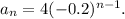
So, the common ratio will be

`r=-0.2~~~\Rightarrow |r|=0.2<1.`

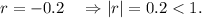
That is, the series will CONVERGE. Option (C) is correct.

For the fourth geometric series, we have

`a_n=0.6(-2)^(n-1).`

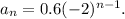
So, the common ratio will be

`r=-2~~~\Rightarrow |r|=2>1.`

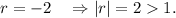
That is, the series will not converge. Option (D) is incorrect.

Thus, (C) is the correct option.

Answer 2

C

Explanation:

A geometric series will only converge if - 1 < r < 1

sum to infinity =
`(a)/(1-r)`

The nth term formula for a geometric series is

`a_(n)` = a
`r^(n-1)`

where a is the first term and r the common ratio

The only summation with - 1 < r < 1 is C where r = - 0.2