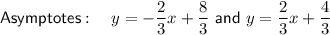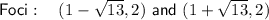Answer:

Explanation:
Given equation:
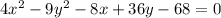
This is an equation for a horizontal hyperbola.
To complete the square for a hyperbola
Arrange the equation so all the terms with variables are on the left side and the constant is on the right side.

Factor out the coefficient of the x² term and the y² term.
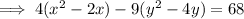
Add the square of half the coefficient of x and y inside the parentheses of the left side, and add the distributed values to the right side:

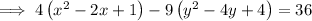
Factor the two perfect trinomials on the left side:
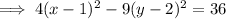
Divide both sides by the number of the right side so the right side equals 1:
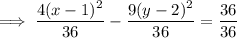
Simplify:

Therefore, this is the standard equation for a horizontal hyperbola with:
- center = (1, 2)
- vertices = (-2, 2) and (4, 2)
- co-vertices = (1, 0) and (1, 4)