Question

Which statements describe the solutions to √x-2 -4=x-6 ? Check all that apply. There are no true solutions to the radical equation. x = 2 is an extraneous solution. x = 3 is a true solution. There is only 1 true solution to the equation. The zeros of 0 = x2 – 5x + 6 are possible solutions to the radical equation.

Answer 1

C, E

Explanation:

got it right on edge

Answer 2

`√(x-2)-4=x-6\\\\√(x-2)=x-6+4\\\\√(x-2)=x-2\\\\ \text{Squaring both sides}\\\\x-2=x^2-4x+4\\\\x^2-4x-x+4+2=0\\\\x^2-5 x+6=0\\\\ \text{Splitting the middle term}\\\\x^2-3x-2x+6=0\\\\x(x-3)-2(x-3)=0\\\\(x-2)(x-3)=0\\\\x=2,3`

Put, x=2 and x=3 in original equation

⇒For, x=2

LHS

`√(2-2)-4\\\\=-4`

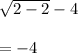
RHS

4-6

= -2

LHS=RHS

Hence, x=2 , is solution of the system.

⇒For , x=3

.LHS=

`√(3-2)-4\\\\=1-4\\\\=-3`

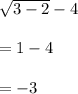
RHS

3-6=-3

Hence, x=3 , is solution of the system.

Option C

x=3, is true solution.

Option E:

The zeros of 0 = x2 – 5x + 6 are possible solutions to the radical equation.