Question

The equation for the circle is: x^2 + y^2 + 16x - 24y + 159 = 0

Answer 1

`{x}^(2) + {y}^(2) + 16x - 24y + 159 = 0 \\ \\ 1. \: x = ( - 16 + 2i √((y - 19)(y - 5)) )/(2) \: ( - 16 - 2i √((y - 19)(y - 5)) )/(2) \\ \\ 2. \: x = - 8 + i √((y - 19)(y - 5)) \: \: - 8 - i √((y - 19)(y - 5))`

Make sure you put a comma between them

Answer 2

____________________________________________________

Answer:

The center would be (-8,12).

____________________________________________________

Explanation:

First,we're going to have to simplify the equation. Here is the work below:

`x^2+y^2+16x-24y+159=0\\\\(x+8)^2-64+y^2-24y+159=0\\\\(x+8)^2+y^2-24y=-159+64\\\\(x+8)^2+(y-12)^2-144=-159+64\\\\(x+8)^2+(y-12)^2=144-159+64\\\\(x+8)^2+(y-12)^2=49\\\\`

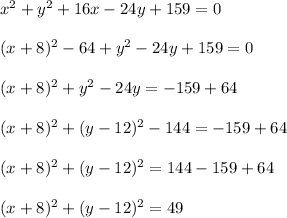
Now, you must use the "form of a circle" equation in order to find out the center and radius of a circle.

The equation is:

`(x-h)^2+(y-k)^2=r^2\\\\r=7\\h=-8\\k=12`

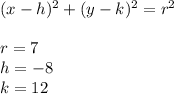
Since we got the answer of:

`(x+8)^2+(y-12)^2=49`

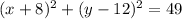
It matches with our equation of
`(x-h)^2+(y-k)^2=r^2`

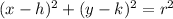
Our "h" represents the x axis on the graph, our "k" represents our y axis on a graph.

Therefore our x value would be -8 and our y value would be 12.

Your FINAL answer should be (-8,12)

____________________________________________________