Answer:
3a. horizontal shift to the left 4 units, reflection on the x-axis
3b. vertical shift down 5 units
4. 4
5. 3x²y²
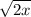
6.
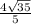
7.
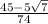
8. 3√2
9. -2√7 + 5√13
10. 7√2 + 2√14
11. 10 + √15 + 2√35 + √21
12. P = 18√6 + 6√15
Explanation:
this is gonna be a bit long but bare with me
3a. y =
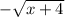< -- this is a horizontal shift to the left 4 units and a reflection on the x-axis. a horizontal shift is located next to the parent function (in this case f(x) = √x). a reflection on the x-axis is located outside of the parent function.
3b. y =
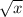- 5 < --- this is a vertical shift down 5 units. a vertical shift is located outside of the parent function
4.
to solve a radicand, we can break it up into known factors, such as numbers that are a perfect square that are factors of the number. you can create a factor tree for this, or you can do it mentally by thinking of terms.
48 can be divided by divided by 16 and 3
16 is a perfect square of 4, which goes outside of the radicand
the answer to
is 4
5. again, to solve
, we break it down into known factors.
lets start with 18: it can be broken down into 9 and 2, 9 is a perfect square of 3
so far the radicand looks like this: 3
next we will break down
. looking at the exponent, we can see that we have a perfect square in the exponent, which is 4. the square root of 4 is 2. we would leave the leftover x in the radical as it is not a perfect square, and put x² on the outside as it is a result of the perfect square
3x²
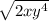
finally lets look at
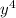. we see that the exponent is a perfect square, 4. the square root of 4 is 2, so y² would go on the outside, and no y terms would be left on the inside. the final radical looks like this:
3x²y²
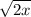
6.
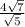
to solve this, we would need to rationalize the denominator by getting rid of the radical in the denominator. to do this we would multiply the expression by
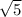and we would get:
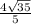
we cannot simplify this any further, so this would be our answer
7.
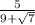like the last question, we need to get rid of the square root in the denominator by multiplying the entire expression by
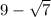. we get:
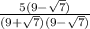
the denominator can be multiplied together to get 81 - 7 = 74, and in the numerator we get 5(9-√7) which can be distributed as 45 - 5√7. in total we get:
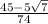this cannot be simplified any further, so this is the answer
8. 3√50 - 3√32 to solve, we need to get the same radical. to do this, we can break each radical up into known terms. √50 can be simplified as 25 and 2. 25 is a perfect square, and is equal to 5. √50 = 5√2
3(5√2) = 15√2
we can break up √32 as 16 and 2. 16 is a perfect square which is equal to 4. √32 = 4√2
-3(4√2) = -12√2
the expression looks like this: 15√2 - 12√2 < subtract normally and we get 3√2 <-- this is our final answer, and we cannot simplify further
9. 2√7 - 4√13 -4√7 + 9√13 < we can combine like terms by adding/subtracting
2√7 -4√7 = -2√7
-4√13 + 9√13 = 5√13
-2√7 + 5√13 this cannot be simplified further, so this is the answer
10. √7(√14 + 2√2) < distribute √7 into the expression
√7 × √14 = √98 = 7√2
√7 × 2√2 = 2√14
the answer is 7√2 + 2√14
11. (√5 + √7)(√20 + √3) < to solve, we can FOIL this out
(√5 + √7)(√20 + √3) = 10
(√5 + √7)(√20 + √3) = √15
(√5 + √7)(√20 + √3) = 2√35
(√5 + √7)(√20 + √3) = √21
we get the following expression: 10 + √15 + 2√35 + √21, we cannot simplify this further so this is our answer
12. the perimeter of a rectangle is P = 2l + 2w. we are given the width 3√6 + 4√15 and the length 6√6 - √15. plugged into the formula we have:
2(3√6 + 4√15) + 2(6√6 - √15) < distribute 2 into each expression:
(6√6 + 8√15) + (12√6 - 2√15) < combine like terms, as in combine terms with like radicals
6√6 + 12√6 = 18√6
8√15 - 2√15 = 6√15
P = 18√6 + 6√15
we cannot simplify this further, so this is the answer
hope this helped!