Question

Miguel has started training for a race. The first time he trains, he runs 0.5 mile. Each subsequent time he trains, he runs 0.2 mile farther than he did the previous time.

a) What is the arithmetic series that represents the total distance Miguel has run after he has trained n times?



b) A marathon is 26.2 miles. What is the least number of times Miguel must run for his total distance run during training to exceed the distance of a marathon?

Answer 1

A) the bottom left is the correct answer (0.3+0.2k)

B) 15 times

Step-by-step explanation

Answer 2

a)
`S_n=(0.4+0.1n)n`

b) 15

Explanation:

The first time Miguel trains, he runs 0.5 mile, so
`a_1=0.5`

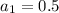
Each subsequent time he trains, he runs 0.2 mile farther than he did the previous time, so
`d=0.2`

Use the formula for nth term of arithmetic sequence

`a_n=a_1+(n-1)d\\ \\a_n=0.5+0.2(n-1)=0.5+0.2n-0.2=0.3+0.2n`

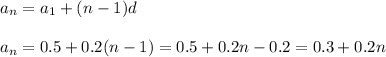
a) The sum of n terms of the arithmetic sequence is

`S_n=(a_1+a_n)/(2)\cdot n\\ \\S_n=(0.5+0.3+0.2n)/(2)\cdot n=(0.4+0.1n)n`

b) A marathon is 26.2 miles, then

`(0.4+0.1n)n\ge 26.2\\ \\0.1n^2+0.4n-26.2\ge 0\\ \\n^2+4n-262\ge 0\\ \\D=4^2-4\cdot (-262)=16+1048=1064\\ \\n_(1,2)=(-4\pm√(1064))/(2)=-2\pm √(266) \\ \\n\in (-\infty,-2-√(266)]\cup[-2+√(266),\infty)`

Since n is positive and
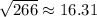`√(266)\approx 16.31`, the least number of times Miguel must run for his total distance run during training to exceed the distance of a marathon is -2+17=15