Answer:
Total area = 135 .39 square yard
Explanation:
Given : composite figure.
To find : Find the surface area of the composite solid. Round the answer to the nearest hundredth.
Solution : We have given a composite figure with rectangle base and four triangles .
Base of two triangle = 4 yd .
Height of two triangle = √13 yd .
Base of other two triangle = 6 yd .
Height of other two triangle = 2√2 yd .
Area of rectangle = length * width .
Area of rectangle = 6 *4
Area of rectangle = 24 square yard .
Area of all rectangle = 3 *24 = 72 square yard
Area of two square = 2( 4*4) = 32 square yard.
Area of triangle =
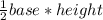 .
.
Area of triangle=
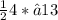 .
.
Area of triangle = 2√13 .
Area of two triangle = 2 * 2√13 .
Area of two triangle = 4√13 square yard.
Area of other triangle =
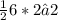 .
.
Area of other triangle = 3* 2√2
Area of other triangle = 6√2.
Area of other two triangle = 2 *6√2.
Area of other two triangle = 12√2 square yard.
Total area = Area of 3 rectangle + Area of two triangle + Area of other two triangle + area of square
Total area = 72 + 4√13 + 12√2 + 32
Total area = 135 .39 square yard.
Therefore, Total area = 135 .39 square yard.