Question

How does jumping into a pool change the amount of gravity acting on you?​

Answer 1

Because of the buoyant force

Step-by-step explanation:

Jumping into a pool change the amount of apparent gravity acting on a person.

Normally, for a person in free fall, the weight of the person is given by:

`F=mg`

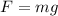
where m is the mass of the person and g=9.8 m/s^ is the acceleration due to gravity.

When a person is in the water, there is a buoyant force pushing the person upward. The magnitude of the buoyant force is

`B=\rho_w V g`

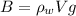
where

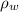`\rho_w` is the density of the water

V is the volume of displaced fluid

g is the acceleration due to gravity

So the net force acting on the person is

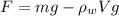`F= mg - \rho_w V g` (1)

Since V corresponds to the volume of the person, we can rewrite it as

`V=(m)/(\rho_p)`

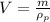
where
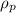`\rho_p` is the density of the person. Substituting into eq.(1),

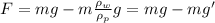`F=mg- m (\rho_w)/(\rho_p) g = mg - mg'` (2)

where we called

`g'=(\rho_w)/(\rho_p) g`

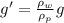
So we can further rewrite (2) as

`F=m(g-g')`

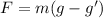
so we see that the gravity acting on the person, g, has been modified into (g-g') due to the presence of the buoyant force.