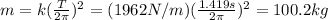Answer:
100.2 kg
Step-by-step explanation:
The period of vibration of a spring-mass system is given by
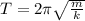
where
T is the period
m is the mass
k is the spring constant
In this problem, we know
T = 1.419 s is the period
k = 1962 N/m is the spring constant
Re-arranging the equation, we can find the mass: