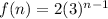Answer:
3;
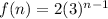
Explanation:
The given sequence is
2, 6, 18, 54,....
The first term is
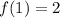
The common ratio is obtained expressing a subsequent term over a previous term.
The common ratio is
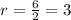
The the nth term of the sequence is given by:
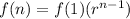
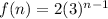
The exponential function which represents the sequence is