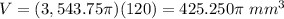Answer:
The volume of the stack is
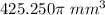
Explanation:
we know that
The volume of the cylinder (DVD stack) is equal to
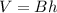
where
B is the area of the base
h is the height of the stack
Find the area of the base B
The area of the base B is equal to the area of the larger circle minus the area of the hollow center
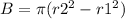
we have
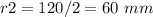 -----> the radius is half the diameter
-----> the radius is half the diameter
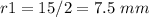 -----> the radius is half the diameter
-----> the radius is half the diameter
substitute
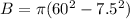
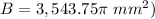
Find the height of the stack
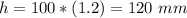
Find the volume