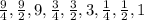Answer:
Potential roots:
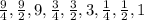
Explanation:
Simply put, the rational roots theorem tells us that if there are any rational roots of a polynomial function, they must be in the form
±
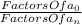
Where
a_n is the number before the highest power of the polynomial, and
a_0 is the constant in the polynomial
From the polynomial shown, we have a_n = 9 and a_0 = 4
The factors of 9 are 9, 3, 1
and
The factors of 4 are 4,2,1
So, if there are any rational roots, they would be:
±
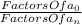
±
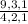
Which is ± 9/4, 9/2, 9/1, 3/4, 3/2, 3/1, 1/4, 1/2, 1/1
or