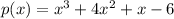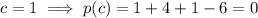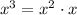 , and
, and
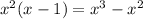 . This gives a remainder of
. This gives a remainder of

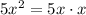 , and
, and
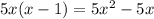 . This gives a new remainder of
. This gives a new remainder of

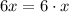 , and
, and
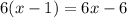 . This gives a new remainder of
. This gives a new remainder of
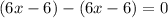
and so there is no remainder.
###
Quicker method: Use the polynomial remainder theorem, which says the remainder upon dividing a polynomial
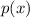 by
by
 is
is
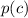 . Here we have
. Here we have