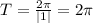Answer:
c. amplitude: 1; period:

Explanation:
The given function is
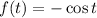
This function is of the form;

where
 is the amplitude.
is the amplitude.
When we compare
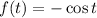 to
to
 , we have
, we have
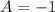 , therefore the amplitude of the given cosine function is
, therefore the amplitude of the given cosine function is
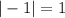
The period is given by;
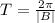
Since B=1, the period is