Question

Find the amplitude and period of f(t)=1/2sin 3t

Answer 1

a. amplitude:
`\displaystyle (1)/(2);`period:
`\displaystyle (2)/(3)\pi`

Step-by-step explanation:

`\displaystyle f(t) = Asin(Bx - C) + D \\ \\ Vertical\:Shift \hookrightarrow D \\ Horisontal\:[Phase]\:Shift \hookrightarrow (C)/(B) \\ Wavelength\:[Period] \hookrightarrow (2)/(B)\pi \\ Amplitude \hookrightarrow |A| \\ \\ Vertical\:Shift \hookrightarrow 0 \\ Horisontal\:[Phase]\:Shift \hookrightarrow 0 \\ Wavelength\:[Period] \hookrightarrow (2)/(3)\pi \\ Amplitude \hookrightarrow (1)/(2)`

With the above information, you now should have an idea of how to interpret graphs like this.

I am joyous to assist you at any time.

Answer 2

Answer: Option A

The Amplitude is

`A = (1)/(2)`

Then the period is

`(2)/(3)\pi`

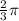
Step-by-step explanation:

The general sine function has the following form

`y = Asin(bx) + k`

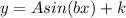
Where A is the amplitude: half the vertical distance between the highest peak and the lowest peak of the wave.

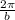`(2\pi)/(b)` is the period: time it takes the wave to complete a cycle.

k is the vertical displacement.

In this case we have the following function

`f(t)=(1)/(2)sin(3t)`

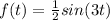
Thus:

`b=3`

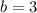
Then the period is

`(2\pi)/(3)=(2)/(3)\pi`

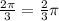
The Amplitude is

`A = (1)/(2)`

The answer is Option A