Question

Find the equation of the line through (6,4) and (-3,-8)

Answer 1

y = 4/3x - 4

Explanation:

to find the equation of a line with 2 points, we use the slope formula which is:

`(y_2-y_1)/(x_2-x_1)`

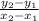
we will use (6,4) as
`x_1[tex] and [tex]y_1` and we will use (-3,-8) as
`x_2[tex] and [tex]y_2`. we plug this into the slope formula:

`(-8-4)/(-3-6)`

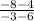
-8 - 4 = -12

-3 - 6 = -9

the slope is
`(-12)/(-9)`

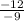
but we can simplify this further by dividing the fraction by -3

-12 / -3 = 4

-9 / -3 = 3

the simplified version of the slope is
`(4)/(3)`

we can write this in slope-intercept form which is y =mx + b, with b being the y intercept and m being the slope

y = 4/3x + b <--- we need to solve for b in order to find the y intercept, so substitute x & y for a point on the line, we can use any point we are given, but for this example i will use (6,4)

4 = 4/3(6) + b < multiply 4/3 x 6

4 = 8 + b < subtract 8 from both sides

-4 = b

our y intercept would be (0,-4)

the equation looks like the following:

y = 4/3x - 4, which is our answer