Question

Find all solutions in the interval [0, 2π).

4 sin2 x - 4 sin x + 1 = 0

Answer 1

`x = (\pi)/(6) \: or \: x = (5\pi)/(6)`

EXPLANATION

The given trigonometric equation is

`4 \sin ^(2) x - 4 \sin(x) + 1 = 0`

This is a quadratic equation in sinx.

We split the middle term to obtain,

`4 \sin ^(2) x - 2 \sin(x) - 2 \sin(x) + 1 = 0`

Factor by grouping to get,

`2 \sin(x) (2 \sin(x) - 1) - 1(2 \sin(x) - 1) = 0`

This implies that,

`(2 \sin(x) - 1)(2 \sin(x) - 1) = 0`

`\sin(x) = 0.5`

This gives us,

`x = (\pi)/(6)`

in the first quadrant.

Or

`x = \pi - (\pi)/(6)`

`x = (5\pi)/(6)`

in the second quadrant.

Answer 2

x =
`(\pi)/(6)`,
`(7\pi)/(6)`,
`(11\pi)/(6)`.

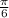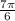Explanation:

The given equation is 4 sin²x - 4 sin x + 1 = 0

(2sinx)² - 2(2sinx) + 1 = 0

(2sinx - 1 )² = 0

Sinx =
`(1)/(2)` ⇒ x = sin⁻¹ (
`(1)/(2)`)

So between the interval [0, 2π] value of x will be
`(\pi)/(6)`,
`(7\pi)/(6)`,
`(11\pi)/(6)`

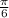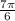[Since sine is positive in 1st 3rd and 4th quadrant]

So value of x will be x =
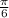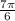`(\pi)/(6)`,
`(7\pi)/(6)`,
`(11\pi)/(6)`.