Question

Find the length of the radius of a circle whose center is at (12, 5 ), and one point on the circle is ( -6, -18 ). Round to the nearest hundredth of the units.

Answer 1

AB = 29.23

Explanation:

Points to remember

Distance formula

Distance between two points (x₁, y₁) and (x₂, y₂) is given by

Distance = √[(x₂- x₁)² + (y₂ - y₁)²]

To find the radius

Center = (12, 5) and point on the circle = (-6, -18)

Radius = √[(x₂- x₁)² + (y₂ - y₁)²]

= √[(12 - - 6)² + (5 - -18)²]

= √[(12 + 6)² + (5 +18)²]

=√[18² + 23²] = √[324 +529 ] = 29.23

Answer 2

Hello!

The answer is:

The radius of the circle is 29.21 units.

Why?

To solve the problem, we need to remember that the radius of a circle is the distance from its center to any point of the circle.

We can use the following equation to calculate the distance between the center and the given point:

`distance=radius=\sqrt{(x_2-x_1)^(2)+(y_2-y_1)^(2) }`

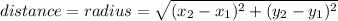
So, we are given the information:

`Center(12,5)\\Point(-6,-18)`

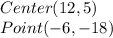
Where,

`x_1=12\\y_1=5\\x_2=-6\\y_2=-18`

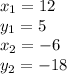
Now, substituting and calculating, we have:

`radius=\sqrt{((-6)-(12))^(2)+((-18)-(5)^(2)}\\\\radius=\sqrt{(-18)^(2)+(-23)^(2)}=√(324+529)=√(853)=29.21units`

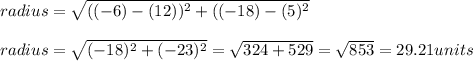
Hence, we have that the radius of the circle is 29.21 units.

Have a nice day!