Question

the Johnsons want to cover their backyard with new grass their backyard is rectangular with a length of 3x - 2 feet and a width of 3x + 1 ft however there rectangular swimming pool along with its surrounding patio has dimensions of x + 4 by x + 5 ft what is the area of the region of the yard that they want to cover with new grass

Answer 1

Hello!

The answer is:

The area that the want to cover with new grass will be:

`Area_(grass)=8x^(2) -12x-22`

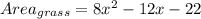
Why?

If we want to calculate what is the ara of the region of the backyard that they want to cover with new grass, we need to calculate the area of the backyard, calculate the area of the swimming pool and its patio, and the last step is to subtract the area of the swimming pool and its patio to the total area of the backyard.

So, to calculate the areas, we need to use the following formula:

`Area=Length*Width`

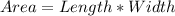
Also, we need to remember how the distributive property works, since we are going to need it.

We have that:

`(a+b)(c+d)=ac+ad+bc+bd`

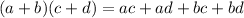
We are given the following information:

For the backyard we have:

`Length=3x-2\\Width=3x+1`

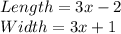
For the swimming pool and its patio:

Since there it's not mentioned, let be the first expression the length, and the second one, the width.

`Length=x+4\\Width=x+5`

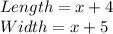
Then, calculating we have:

Backyard:

`Area_(backyard)=(3x-2)*(3x+1)=9x^(2)+3x-6x-2=9x^(2)-3x-2`

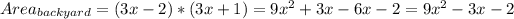
Swimming pool and patio:

`Area_(swimmingpool)=(x+4)*(x+5)=x^(2)+5x+4x+20=x^(2)+9x+20`

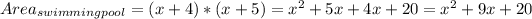
Now, calculating the area that they want to cover with new grass, we have:

`Area_(grass)=Area_(backyard)-Area_(swimmingPool)\\\\Area_(grass)=(9x^(2)-3x-2)-(x^(2)+9x+20)\\\\Area_(grass)=9x^(2) -x^(2) -3x-9x-2-20\\\\Area_(grass)=8x^(2) -12x-22`

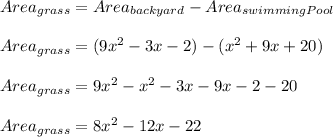
Hence, we have that the area that the want to cover with new grass will be:

`Area_(grass)=8x^(2) -12x-22`

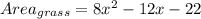
Have a nice day!